​
Optimizing Maritime Operations Using Reinforcement Learning

Data Science Team, SIYA
August 6, 2023
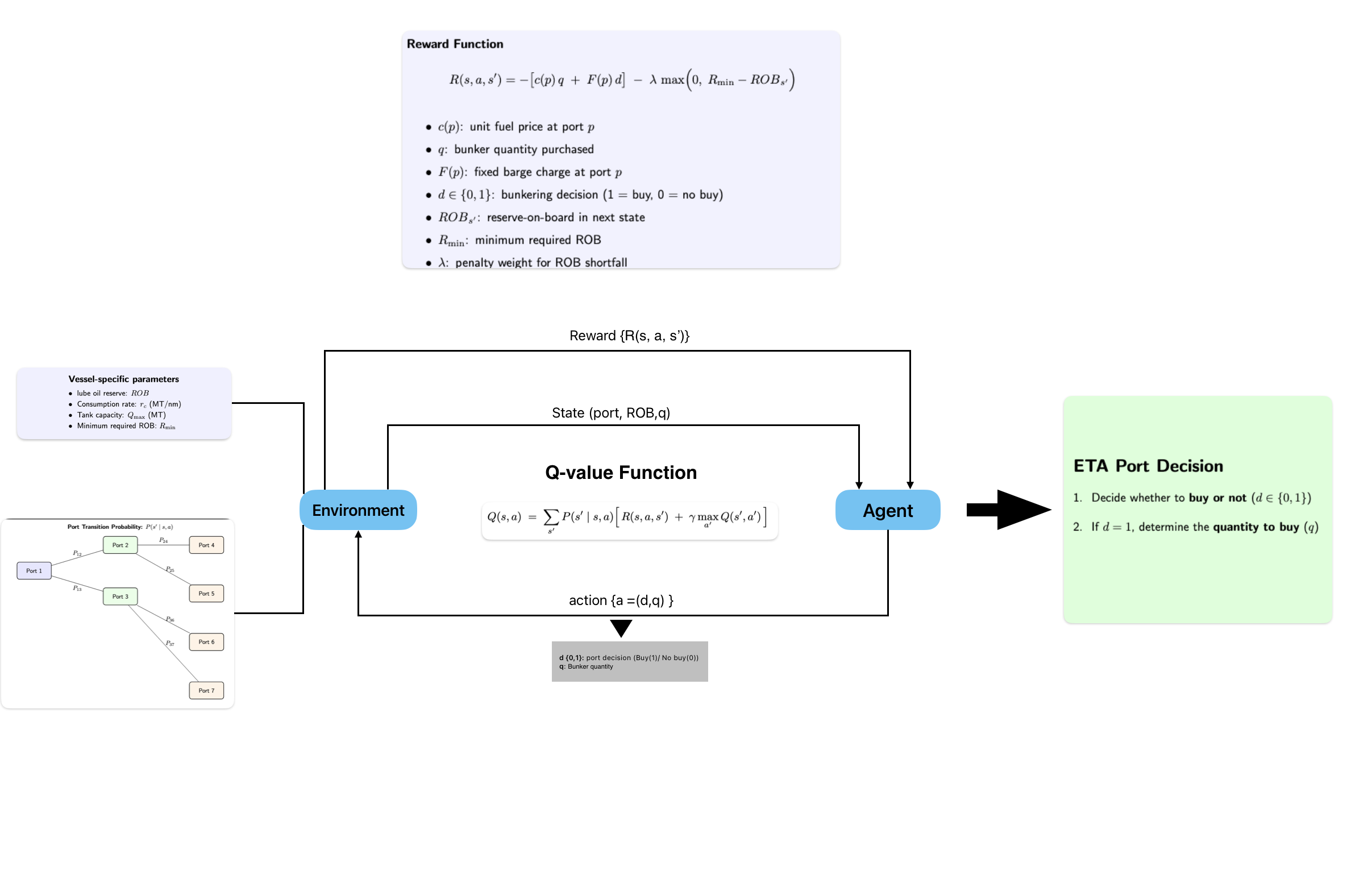
Reinforcement Learning for Maritime Operations Optimization

Q-Learning Workflow for Lube Oil Optimization

​
Abstract

In this paper, we investigate the transformative potential of reinforcement learning (RL) in the maritime industry, with a focus on optimizing operational efficiency and reducing costs. Our team has explored multiple use cases of RL, placing primary emphasis on a cost-efficient lube oil refill strategy for vessels. Utilizing the Q-learning algorithm, we developed a model that optimizes lube oil refills by considering various operational parameters, including consumption rates, port distances, and refilling costs. Our results demonstrate the model’s effectiveness in minimizing operational costs while ensuring sufficient lube oil availability. Additionally, we discuss other promising applications of RL in maritime operations, such as route optimization, fuel management and predictive maintenance. This research showcases the broad applicability and significant benefits of RL in enhancing maritime operational efficiency.

​
1. Introduction

The maritime industry continuously seeks innovative solutions to optimize operations and reduce costs. Reinforcement learning (RL), a subfield of machine learning, offers promising techniques to achieve these goals. This paper provides an overview of RL applications in the maritime industry, highlighting research conducted by our team and presenting a detailed use case utilizing the Q-learning algorithm to optimize the lube oil refill strategy.

​
2. Reinforcement Learning in Maritime Industry

Reinforcement learning has significant potential in various maritime applications. Our team at Synergy Marine Group has explored several key areas:

​
Route Optimization

We have researched RL algorithms to find the most cost-effective and safest shipping routes by considering factors such as fuel consumption, weather conditions, and port congestion. This research aims to enhance route efficiency and reduce travel time.

​
Fuel Management

Optimizing fuel consumption based on vessel speed, load, and sea conditions is another area of our research. RL can learn optimal fuel usage patterns, leading to significant fuel savings and reduced emissions.

​
Predictive Maintenance

Our team is investigating RL for predictive maintenance of ships and port equipment. By analyzing sensor data and historical maintenance records, RL can predict maintenance needs, reducing downtime and maintenance costs.

​
Lube Oil Refill Strategy

The reinforcement learning model frames the problem as a Markov Decision Process (MDP). The model learns to make decisions by interacting with the environment, aiming to minimize the total cost while ensuring the lube oil Remaining On Board (ROB) is sufficient. This paper presents a detailed use case where the Q-learning algorithm is used to optimize the lube oil refill strategy for a vessel.

​
3. Cost-Efficient Lube Oil Refill Strategy for Vessels

​
3.1 Parameters and Environment Setup

The model considers various parameters and environmental factors, such as:
  • Average per hour consumption of lube oil by the vessel
  • Speed of the vessel
  • Tank capacity
  • Possible next ports and their probabilities
  • Price of lube oil at each port
  • Delivery charges and policies at each port
  • Distances between possible port pairs
  • Minimum required ROB
  • Maximum quantity of fuel that can be refilled at a port

​
3.2 MDP Formulation

States: The state represents the current lube oil ROB and the vessel’s location. Actions: The actions are the possible amounts of lube oil to refill at each port. Rewards: The reward is the negative of the cost incurred for refilling lube oil. This encourages the model to minimize costs. Transition probabilities: The transition probabilities are based on the predicted probabilities of visiting the next port.

​
3.3 Reward Function

Let:
  • pp: current port
  • c(p)c(p): unit price of lube oil at port pp
  • qq: bunker quantity purchased (MT)
  • F(p)F(p): fixed barge/delivery charge at port pp
  • d∈{0,1}d \in \{0,1\}: bunkering decision (1 = buy, 0 = no buy)
  • ROBs′ROB_{s'}: reserve-on-board in the next state
  • Rmin⁡R_{\min}: minimum required ROB
  • λ\lambda: penalty weight
To incorporate the effect of distance and consumption rate, the reward function is adjusted to include the cost of lube oil and the consumption cost based on the distance traveled. The updated reward function is: R(s,a,s′)=−[c(p) q+F(p) d]−λmax⁡(0, Rmin⁡−ROBs′)R(s,a,s') = -\Big[c(p)\,q + F(p)\,d\Big] - \lambda \max\Big(0,\, R_{\min} - ROB_{s'}\Big)

​
3.4 Q-Learning Algorithm

The Q-learning algorithm is used to train the reinforcement learning model. The Q-value is updated using the following equation: Q(s,a)←Q(s,a)+α[r+γmax⁡a′Q(s′,a′)−Q(s,a)]Q(s, a) \leftarrow Q(s, a) + \alpha \Big[ r + \gamma \max_{a'} Q(s', a') - Q(s, a) \Big] where:
  • Q(s,a) is the Q-value for state s and action a
  • α is the learning rate
  • R is the reward received after taking action a in state s
  • γ\gamma is the discount factor
  • s’ is the next state
  • a’ is the action that maximizes the Q-value in the next state
The Q-values are updated based on the observed rewards and the estimated future rewards using the Q-learning update rule. This iterative process helps in finding the optimal refill strategy over multiple episodes.

​
Pseudocode

Initialize Q(s, a) arbitrarily for all states s and actions a
For each episode:
    Initialize state s = (starting_port, ROB)
    Set max_delta = 0   # track maximum Q-value change in this episode

    For t = 1 to N:   # N ports in the episode

        # Step 1: Action Selection
        Choose action a = (d, x_i) from state s using ε-greedy policy
            d ∈ {0, 1}   # decision: buy or not
            x_i = quantity of lube oil to bunker at port i if d = 1

        # Step 2: Transition
        Sample next port j ~ q_j   # based on transition probabilities
        Compute oil consumed = r_c * d_ij
        Update ROB' = ROB - oil_consumed + x_i (if d = 1)

        # Step 3: Reward Calculation
        Compute reward:
        R(s, a, s') =
            - [ c_i * x_i + F(i) * d + Σ_j q_j (r_c * d_ij * c_j) ]
            - λ * max(0, R_min - ROB')

        # Step 4: Q-value Update
        old_Q = Q(s, a)
        Q(s, a) ← Q(s, a) + α [ R(s,a,s') + γ max_{a'} Q(s', a') - Q(s, a) ]
        delta = |Q(s, a) - old_Q|
        max_delta = max(max_delta, delta)

        # Step 5: State Transition
        s ← (j, ROB')

    End For

    # Check for episode-level convergence
    If max_delta < ε_converge:
        Break   # Q-values have converged, stop episode loop

End For

​
3.5 Implementation

The Q-learning algorithm is implemented by initializing the Q-table with all zeros. Various hyperparameters were experimented with to reach the optimal algorithm. A range of learning rates α (0.1, 0.3, 0.5) and discount factors γ (0.9, 0.95, 0.99) were used over multiple runs. The number of episodes was set to 10,000, and the convergence threshold was defined as the point where the change in Q-values was less than 1e⁻⁶ for 1,000 consecutive episodes. The process started from a random state, selected an action using the epsilon-greedy policy, took the action, and observed the reward and next state. The Q-value was then updated using the Q-learning update rule. This iterative process continued until the algorithm converged to an optimal strategy.

​
3.6 Usage of the Model

The model can be used to determine the optimal refill strategy given the current port and the remaining onboard (ROB) lube oil. Here’s how it works:
  • Given the current port and the ROB, the model predicts the optimal ports for lube oil refilling
  • It provides the possible ports from where lube oil refill should be done and the quantity of refill required
  • The model also outputs the cost of refilling at each recommended port, considering the possible routes, associated costs, probabilities, and distances

​
3.7 Results and Discussion

The results demonstrate the effectiveness of the Q-learning algorithm in optimizing the lube oil refill strategy. The model successfully minimizes the total cost by making informed decisions on when and how much to refill at each port.

​
4. Conclusion

Reinforcement learning offers significant potential to optimize various aspects of maritime operations. The primary use case presented in this paper illustrates how Q-learning can be used to optimize the lube oil refill strategy, resulting in substantial cost savings. Our ongoing research explores other applications of RL in the maritime industry to further enhance operational efficiency and reduce costs.